ESR11 - Highly parallel solvers for contact problems with friction
Recruiting Institution/Company: Vysoka Skola Banska – Technicka Univerzita Ostrava (Czech Republic)
PhD awarded by: Vysoka Skola Banska – Technicka Univerzita Ostrava (Czech Republic)
One of the most thought-provoking tasks associated with the analysis of rotordynamic systems is the numerical modelling of the contacts. These problems are difficult to formulate and solve because of the non-linearity associated with the relations between displacements or rates of displacements and forces on a part of the boundary which is usually governed by tribological laws. The discretization of such problems leads to very large and ill-conditioned systems. Such systems can be transformed by dualization theory to smaller better-conditioned systems and solved by employing domain decomposition methods with asymptotically linear complexity.
The important advantage of applying the FETI procedure to the contact problems without friction is that, in addition to duality reducing the dimension of the original problem, it also turns all the inequality constraints into bound constraints. Also, FETI methods provide numerical scalability for the problem. Even though the resulting QP problem has bound constraints along with the equality constraints, the resulting problem is still easier to solve compared to the contact problems in displacements. In this project, different formulations for the contact problem relevant for systems like component interaction in turbines are investigated and compared. In particular, techniques allowing to rewrite the difficult quadratic problem including inequalities into standard quadratic problems for domain decomposition are investigated.
Different methods are used to solve benchmark quadratic programming problems and compared to understand the difference in the performance of the algorithms. The first problem is a basic one-dimensional string system with unit length having box constraints and different loads. The second benchmark problem comprises a two-dimensional membrane having forces acting on the membrane and lower and upper obstacles which play the role of the box constraints.
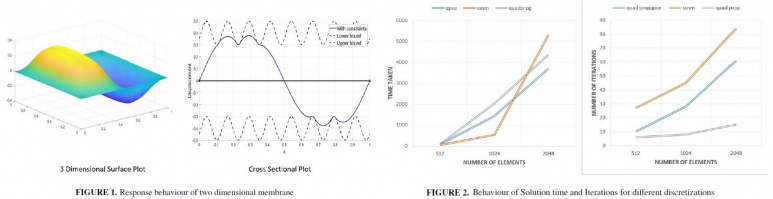
As the number of elements increases and the problem becomes more complex, the variation in the solving capacity of different solvers becomes clear and distinct. Comparison of solvers used for solving problems with contact was essential in understanding the working of different types of algorithms. It gave an idea regarding ways to approach and solve some basic benchmarks of contact problems depending on their constraints. Also, the knowledge of the numbers of iterations and their costs for different algorithms gave us the realization of employing methods like domain decomposition and parallel programming techniques which can guide us in considerably reducing the time and cost of solving larger problems in a very effective manner.
